| Complete
Solution:
There are several ways to approach this
problem.
The table shows all the possibilities if
the checks are labeled a, b,
and c, and the corresponding envelopes A,
B, and C. There are six different
possibilities, each one of them equally likely.
| A |
B |
C |
| a |
b |
c |
| a |
c |
b |
| b |
a |
c |
| b |
c |
a |
| c |
a |
b |
| c |
b |
a |
Only one, however, has all three checks in the matching
envelopes. Since exactly 1 case out of 6 has the checks
in the correct envelopes, the probability is 1/6.
Alternate Approach
1:
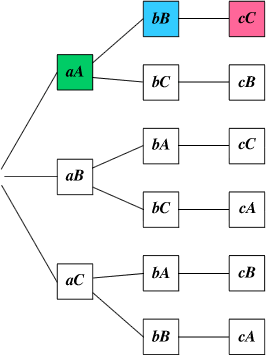
Draw a tree diagram. In the following diagram, aA
indicates that check a is in envelope A.
Like the table shown earlier, the tree diagram indicates
that there is only 1 correct outcome out of 6 equally
likely possibilities. Therefore, the probability of the
correct placement is 1/6.
Alternate Approach
2:
You also can consider the problem geometrically. Draw
a rectangle like the one below to represent all the possibilities
in this situation. Because the chance that the first check
is placed in the correct envelope is 1 in 3, shade 1/3
of the rectangle to indicate this outcome.

If the first check is placed correctly,
there are only two possible envelopes for the second check.
This means that the chance that the second check is placed
in the correct envelope is 1 in 2. To indicate this outcome,
darken 1/2 of the previously shaded area.

If the first two checks are placed correctly,
then the final check also must be placed in the correct
envelope. No further shading is necessary. The darker
shading represents 1/6 of the entire rectangle, so the
probability that all three checks are placed correctly
is 1/6. |