Answer:
There are 64,000 different combinations for the lock.

Complete Solution:
In the challenge, the lock uses the numbers 0 to 39. Start with an easier problem using 1, 2, and 3. You can count the possibilities by drawing a tree diagram. A portion of this tree diagram is shown below:

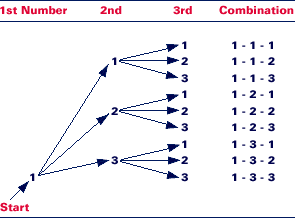
If you start with 1, you get nine different combinations. If you start with 2 instead of 1, you also get nine different combinations. If you start with 3, you get nine more possibilities for a total of 9 + 9 + 9 = 27 different combinations.

Think about this in terms of choices. You can choose any of three numbers as a possible first number in the combination, follow that with a choice of any of the three numbers as the second number in the combination, and finally choose any of the three numbers for the final number in the combination for a total of 3 × 3 × 3, or 27 different combinations.

If the lock used the numbers 1, 2, 3, and 4, you would have to choose from four numbers, three different times. This would give you 4 × 4 × 4, or 64 choices for the combination. The lock in the challenge requires that you choose from 40 different numbers, three different times. Therefore, there are 40 × 40 × 40, or 64,000 different combinations.