Quick Answer:

Two possible solutions are show here:

Complete Solution:

There are many ways to approach this problem. Assuming that all pieces of the cake have the same height, the size (or volume) of each piece depends on the area of its top. Since icing is on both the top and the sides, however, each piece must also have an equal share of the perimeter of the square. If six people share the whole cake, then three people will share half the cake. One way to divide the cake in half is shown here.

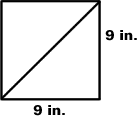
Each half of the cake is 18 inches on its two outer edges. So each person should receive 18/3, or 6 inches, of the cake’s outer edge. One way to make this division is shown below:

To check the areas of the three pieces, use the formula for the area of a triangle:

Area = (1/2) base × height

The height of triangles 1 and 3 in the diagram is half the width of the cake, or 4.5 inches. Since the length of each base is 6 inches, the area of each of these two triangles is:

A = (1/2) × 6 × 4.5 = 13.5 in²

The area of shape 2 is half the area of the entire cake, minus the area of triangles 1 and 3:

Area of half = (1/2) × 9 × 9 = 81/2
= 40.5, or 40.5 in²

AreaTriangle1 = AreaTriangle3
= (1/2) × 6 × 4.5 = 13.5, or 13.5 in²

AreaRegion2 is Area of half of the cake
– AreaTriangle1 – AreaTriangle3

AreaRegion2 = (1/2) × 9 × 9 –13.5 – 13.5 = 13.5, or 13.5 in²

Therefore, these three pieces represent equal shares. The other half of the cake can be divided similarly.

There are other ways to cut the cake into six equal shares. For example, you could start by dividing the cake into two rectangles of the same size and shape.