| There are several ways to solve this
problem. Using the hint, one table can seat four people.
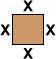
Adding another table takes away one place and adds three
places for a net gain of two seats.
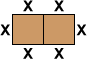
Reasoning in this way, when an additional table is added,
one seat is lost and three are gained for a net gain of
two. Continuing for three, four, and so on, at least nine
tables are required to seat 19 people. There are many
different possible arrangements of the tables.
Alternate Solution #1:
Another way is to make a chart and look for patterns.
| Number
of Tables |
Number
of
People Seated |
| 1 |
4 |
| 2 |
6 |
| 3 |
8 |
| ... |
... |
The pattern indicates an increase of two seats each time.
Continuing the pattern, nine tables will seat 20 people
but eight will only seat 18. Thus, nine tables are required
for 19 people.
Alternate Solution #2:
Thinking geometrically leads to a general rule for the
seating pattern. For every table arrangement, you can
always seat one "at each end" with as many people
on each side as there are tables.
Examples:

With the two people at the ends and twice the number
of people as there are tables seated at the sides, a general
rule for n tables would allow seating a maximum of 2 +
2n people.
For 19 people,
This means that at least nine tables must be used. |