| The
lines in the drawing show one path of a hole-in-one. The
marked angles (1 and 2) have equal size. You should aim
for point P.
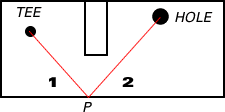
|
One way to locate the proper place to
aim is to think of the sidewall as a mirror. If you looked
into this mirror from the tee, the hole's reflection would
appear to be in the location shown in the diagram below:
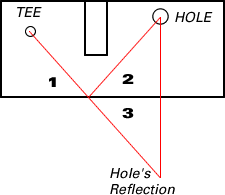
As mentioned in the hint, the angle at which the ball
leaves the wall will be the same as the angle at which
it hit the wall. If you aim the ball at the point where
the line from the tee to the hole’s image intersects
the wall, then it will bounce into the hole.
This can be proven mathematically as follows: Because
the two triangles on either side of the wall in the diagram
are mirror images, they are exactly the same size and
shape (congruent). This means that angle 2 is the same
size as angle 3. Angle 1 and angle 3 are also the same
size, because they are vertical angles. (Vertical angles
are angles formed by two intersecting lines.) Angle 1
is the same size as angle 2 because both are the same
size as angle 3. This means that the path to the hole
shown on the diagram is the same path the ball will take
as it bounces off the wall. |