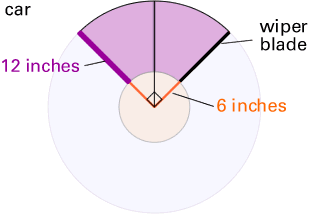
| The car wiper rotates through 1/4 (or
one quarter) of a circle. The area cleaned is the difference
in the areas of two quarter-circles as shown below:
The area of a circle may be found using the following
formula:

The wiper arm swings through an arc of 90°,
or 1/4 of a circle. The area of a quarter-circle can be
found by multiplying the area of the corresponding circle
by 1/4. In this case, the area cleaned by the wiper is
the area of the bigger quarter-circle minus the area of
the smaller one. The radius of the big circle is 6 + 12,
or 18 inches. The radius of the small circle is 6 inches
so that the area cleaned is:

The area of the shape cleaned
by the truck wiper is really the same as a rectangle.
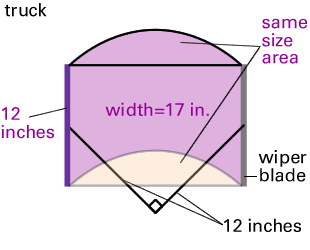
The curved area at the top of the shape
is the same size as the part at the bottom that is not
cleaned by the wiper. The height of the rectangle is determined
by the size of the wiper: 12 inches. The width of the
rectangle can be found by drawing the figure to scale,
then measuring, or by using the Pythagorean theorem. According
to the Pythagorean theorem, the sum of the squares
of the two shorter sides of a right triangle equals the
square of the longest side, thus:
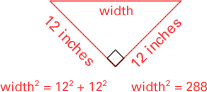
Therefore, the width of the rectangle is
the square root of 288, or approximately 17 inches. The
area of a rectangle can be found by multiplying its height
and its width. In this case, the area is about 17 ×
12, or 204 square inches. This is less than the area cleaned
by the car wiper. |